Ingvar Kullberg
2006-09-04 10:25:55 UTC
In article 27, Compasses, in my chaotic series of
fractal articles,
http://klippan.seths.se/fractals/articles
I've made a generalisation of the cubic iteration
formula, z -> z^3 - 2a^2 z + b to z -> z^d - 2a^(d-1) z
in order to see what happens when d = 2, 3, 4, 5, etc,
the a-plane plotted, b is fixed to zero, and z
initialised to "a", which always is at least one
of the critical points. More about this can be
read in the article referred to above. Why this
formula is called "Compasses" will be obvious
when looking at the illustrations. I've written the
formula so you can put "d" as ANY REAL AND COMPLEX
NUMBER. The results in these later cases are very
amazing and interesting.
NOW I HAVE made this iteration formula complete,
in as much I've added the second parameter "b",
i e we iterate z -> z^d - 2a^(d-1) z + b, the
parameters (a, b), forming a four dimensional
hyper space. In this formula, ExtendedCompasses,
you can plot all 6 system of slices, and even
make rotations between the planes in the same way
as in Cubic Parameterspace3, written by my dear
friend Stig Pettersson. My new formula, included
in the ik3-folder, as well as the modules of Stig,
startup-parameter, and pdf-manual can be downloaded
from:
http://klippan.seths.se/fractals/articles/modules.zip
You will always find copies of the ordinary (quadratic)
Mandelbrot set surrounded by more or less crazy
patterns in some areas! Below some illustrations
(b = 0, so the motives could be drawn by the old
"Compasses" as well):
Loading Image...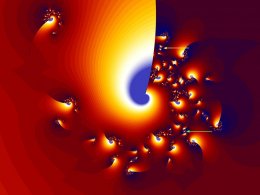
The above motive is a detail when the exponent
d = -4.54545354+1.875778i. The numbers before
the real and imaginary part were typed down by
me when I were in some kind of transcendental mode.
The next motive
Loading Image...
is zoomed in at the spot pointed out by the yellow
arrow in the top of the motive. The below motive
Loading Image...
is zoomed in at the spot pointed out by the green
arrow at the bottom of the motive. The four-armed
star in the middle seems to denote a place where
there ought to be a minibrot! No filters are used,
I promise.
The UF-parameter file for the first motive is at
the very end of this article. Having run this, the
two following motives can easily be found by zooming
at the spots denoted by the arrows. Even the un-
magnified fractal (I call it "parent fractal")
Loading Image...
can easily be found by simply outzooming.
Play, use a high bailout, and move carefully
along the non plotted axis'!
The next article, I hope it will be published within
the nearest future, deals with some ghost like
phenomena I've found when playing with this formula.
--------------------------
Regards,
Ingvar
www.come.to/kullberg
LovelyBrot {
fractal:
title="LovelyBrot" width=640 height=480 layers=1
credits="Ingvar Kullberg;9/1/2006"
layer:
method=multipass caption="Background" opacity=100
mapping:
center=1.149972209735855/0.273915609240573 magn=341141.33
formula:
maxiter=50000 filename="ik3.ufm" entry="ExtendedCompasses"
p_PlottedPlane="1.(a-real,a-imag)" p_hide=yes p_areal=0.0
p_aimag=0.0 p_breal=0.0 p_bimag=0.0 p_xrot=0.0 p_yrot=0.0
p_xrott=0.0 p_yrott=0.0 p_zrot=0.0 p_exponent=-4.54545354/1.875778
p_LocalRot=no p_diff=no p_bailout=100000000 p_dbailout=1E-6
inside:
transfer=none
outside:
density=2 transfer=linear
gradient:
smooth=yes index=0 color=8716288 index=100 color=16121855 index=200
color=46591 index=300 color=156
opacity:
smooth=no index=0 opacity=255
}
fractal articles,
http://klippan.seths.se/fractals/articles
I've made a generalisation of the cubic iteration
formula, z -> z^3 - 2a^2 z + b to z -> z^d - 2a^(d-1) z
in order to see what happens when d = 2, 3, 4, 5, etc,
the a-plane plotted, b is fixed to zero, and z
initialised to "a", which always is at least one
of the critical points. More about this can be
read in the article referred to above. Why this
formula is called "Compasses" will be obvious
when looking at the illustrations. I've written the
formula so you can put "d" as ANY REAL AND COMPLEX
NUMBER. The results in these later cases are very
amazing and interesting.
NOW I HAVE made this iteration formula complete,
in as much I've added the second parameter "b",
i e we iterate z -> z^d - 2a^(d-1) z + b, the
parameters (a, b), forming a four dimensional
hyper space. In this formula, ExtendedCompasses,
you can plot all 6 system of slices, and even
make rotations between the planes in the same way
as in Cubic Parameterspace3, written by my dear
friend Stig Pettersson. My new formula, included
in the ik3-folder, as well as the modules of Stig,
startup-parameter, and pdf-manual can be downloaded
from:
http://klippan.seths.se/fractals/articles/modules.zip
You will always find copies of the ordinary (quadratic)
Mandelbrot set surrounded by more or less crazy
patterns in some areas! Below some illustrations
(b = 0, so the motives could be drawn by the old
"Compasses" as well):
Loading Image...
The above motive is a detail when the exponent
d = -4.54545354+1.875778i. The numbers before
the real and imaginary part were typed down by
me when I were in some kind of transcendental mode.
The next motive
Loading Image...
is zoomed in at the spot pointed out by the yellow
arrow in the top of the motive. The below motive
Loading Image...
is zoomed in at the spot pointed out by the green
arrow at the bottom of the motive. The four-armed
star in the middle seems to denote a place where
there ought to be a minibrot! No filters are used,
I promise.
The UF-parameter file for the first motive is at
the very end of this article. Having run this, the
two following motives can easily be found by zooming
at the spots denoted by the arrows. Even the un-
magnified fractal (I call it "parent fractal")
Loading Image...
can easily be found by simply outzooming.
Play, use a high bailout, and move carefully
along the non plotted axis'!
The next article, I hope it will be published within
the nearest future, deals with some ghost like
phenomena I've found when playing with this formula.
--------------------------
Regards,
Ingvar
www.come.to/kullberg
LovelyBrot {
fractal:
title="LovelyBrot" width=640 height=480 layers=1
credits="Ingvar Kullberg;9/1/2006"
layer:
method=multipass caption="Background" opacity=100
mapping:
center=1.149972209735855/0.273915609240573 magn=341141.33
formula:
maxiter=50000 filename="ik3.ufm" entry="ExtendedCompasses"
p_PlottedPlane="1.(a-real,a-imag)" p_hide=yes p_areal=0.0
p_aimag=0.0 p_breal=0.0 p_bimag=0.0 p_xrot=0.0 p_yrot=0.0
p_xrott=0.0 p_yrott=0.0 p_zrot=0.0 p_exponent=-4.54545354/1.875778
p_LocalRot=no p_diff=no p_bailout=100000000 p_dbailout=1E-6
inside:
transfer=none
outside:
density=2 transfer=linear
gradient:
smooth=yes index=0 color=8716288 index=100 color=16121855 index=200
color=46591 index=300 color=156
opacity:
smooth=no index=0 opacity=255
}